For (100) surfaces, the surface normal is along a (100) direction i.e. the cube axes. For a cubic system, all three axes are equivalent and we will pick the surface normal along the z direction.

Thhe first step is to find a supercell consisting of layers parallel to the surface. The supercell lattice vectors are integer linear combinations of the original lattice vectors. Specifically, we need to find the smallest integer linear combinations that satisfy:

Two superlattice vectors are perpendicular to the surface normal (i.e. in-plane)
The third superlattice vector is parallel to the surface normal

Once again, the original face-centered cubic lattice vectors (in columns) are:

    /  0  a/2 a/2 \
R = | a/2  0  a/2 |
    \ a/2 a/2  0  /

For the 100 surface, we can get a superlattice vector along the z direction by adding the first two columns and subtracting the last column, which corresponds to a linear combination [ 1 1 -1 ]. We now need two linearly-independent superlattice vectors with no z component. The third column i.e. combination [ 0 0 1] already satisfies this criterion, and we can get another from the difference of the first two lattice vectors i.e. the linear combination [ 1 -1 0 ]. Putting these linear combination together along columns, we get the lattice transformation matrix:

    / 0  1  1 \
M = | 0 -1  1 |
    \ 1  0 -1 /

Multiplying the original lattice vectors R by this transformation matrix, we would get the superlattice vectors:

               /  0  a/2 a/2 \   / 0  1  1 \   / a/2 -a/2  0 \
Rsup = R . M = | a/2  0  a/2 | . | 0 -1  1 | = | a/2  a/2  0 |
               \ a/2 a/2  0  /   \ 1  0 -1 /   \  0    0   a /

Note that these superlattice vectors are all perpendicular to each other, with the first two in the x-y plane and the third along z, as desired. The absolute orientation of the lattice vectors in space do not matter, we only need to preserve their lengths and the angles between them. Specifically the above is a tetragonal lattice with square side a/sqrt(2) and height a, which we could specify using a shorthand in JDFTx as

latttice Tetragonal ${aBySqrt2} ${a}  #With a/sqrt(2) and a set previously

The determinant of the transformation matrix, det(M) = 2, which means that det(Rsup) = 2 det(R), or that the volume of the supercell is twice that of the unit cell. Therefore we would need two atoms per supercell, to get the original crystal again. We can leave the first atom at fractional coordinates [ 0 0 0 ] in the unit cell. We can add the second atom at any of the original lattice vectors which has a non-zero component along the surface normal direction.= eg. [ 1 0 0 ] in the unit cell. Now we need to transform these fractional coordinates from the unit cell to the supercell, using the inverse of the transformation matrix, inv(M). The first atom coordinates [ 0 0 0] of course transform to [ 0 0 0 ], and for the second atom, the new coordinates are:

         / 1 \    / 1/2  1/2  1 \   / 1 \   / 1/2 \
inv(M) . | 0 | =  | 1/2 -1/2  0 | . | 0 | = | 1/2 |
         \ 0 /    \ 1/2  1/2  0 /   \ 0 /   \ 1/2 /

Therefore, the fractional atom coordinates for the supercell can be specified as:

ion Pt  0.0  0.0  0.0   1
ion Pt  0.5  0.5  0.5   1

At this stage, we have the lattice and ionpos for a supercell calculation. Running JDFTx on this geometry (with appropriate k-point sampling etc.) would give you exactly the same material properties as on the original unit cell, except that extensive properties like the total energy would be twice as large since there are two atoms per unit cell (try it).

Our current supercell has two layers with a 100 surface direction. The next step is to increase the number of layers, and cleave the crystal by adding some gap along the to-be non-periodic third direction. Let's say we want 5 atomic layers, and a minimum gap of 15 bohrs as before. The layer spacing is a/2 (third supercell lattice vector has length a, and there are two layers per supercell so far) = 3.705 bohrs, so 5 empty atomic layers is the minimum number > 15 bohrs of spacing. Therefore we pick a supercell that has 10 atomic layers i.e. five times as before. For this, we scale up our third lattice vector by five:

#Save the following to 100.lattice:
lattice Tetragonal 5.23966 37.05    #a/sqrt(2) and 5a in bohrs, respectively

The third fractional coordinates of the atom would then scale down by a factor of five:

ion Pt  0.0  0.0  0.0   1
ion Pt  0.5  0.5  0.1   1

and we need to repeat this with offsets of 1/5, 2/5 etc. along the third direction. This would produce layers with the third coordinate ranging from 0.0 to 0.9; using periodiocity we can wrap third coordinates in the range [0.5,1) to the range [-0.5,0). Finally, selecting the central five layers, we arrive at the coordinates:

#Save the following to 100.ionpos:
ion Pt  0.0  0.0 -0.2   1
ion Pt  0.5  0.5 -0.1   1
ion Pt  0.0  0.0  0.0   1
ion Pt  0.5  0.5  0.1   1
ion Pt  0.0  0.0  0.2   1

We can quickly test the geometry without running a full calculation. Setup a dummy input file:

#Save the following to testGeometry.in
include ${surface}.lattice   #we will use the same input file later for 110 and 111
include ${surface}.ionpos
ion-species GBRV/$ID_pbe.uspp
#Not a real calculation; missing kpoints and fillings!

and run JDFTx using the dry-run (-n) commandline switch:

export surface="100"   #or "110" or "111" later on
jdftx -ni testGeometry.in | tee testGeometry-${surface}.out

Examine the output file: it performs initialization and quits. We can create an XSF file even from this initialization-only output file as usual:

createXSF testGeometry-${surface}.out ${surface}.xsf

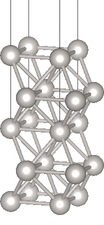
and visualize 100.xsf using VESTA to get an image as shown at the top of the page.

Note that you should adjust the boundary settings, particularly for the z direction to [-0.5,0.5), in order to not tear the visualization across periodic boundaries. You could also repeat the x and y directions by more units say [0,2) or [0,3) to more clearly see the surfce structure (not included in the image shown above).