We need to first find appropriate superlattice vectors starting from the face-centered cubic lattice vectors:

    /  0  a/2 a/2 \
R = | a/2  0  a/2 |
    \ a/2 a/2  0  /

as discussed in detail in the Pt(100) setup page.

For a (111) surface, we want the surface normal along a direction which combines all three cubic axes with equal coefficients. The most obvious combination for this is [ 1 1 1 ], which combines all three face-centered cubic lattice vectors with equal coefficients as well. Check that the combinations [ 0 -1 1 ] and [ 1 0 -1 ] produce superlattice vectors which are orthogonal to the [ 1 1 1 ] combination. This yields the lattice transformation matrix:

    /  0  1  1 \
M = | -1  0  1 |
    \  1 -1  1 /

and the superlattice vectors:

        /   0  -a/2  a \
Rsup =  |  a/2   0   a |
        \ -a/2  a/2  a /

Note that this time, the first two lattice vectors are orthogonal to the third (required), but not to each other. The in-plane lattice vectors instead have an angle of 120 degrees between them. (Their dot product divided by their lengths gives you the cosine.) For the 111 surface, this is the optimum super-cell and orthogonal in-plane lattice vectors are only possible with a larger less-efficient supercell (with more than one atom per layer). To sumamrize, we have the first two superlattice vectors of equal length a/sqrt(2) = 5.23966 bohrs at a 120 degree angle, and a third of length sqrt(3)a = 12.8345 bohrs at right angles to the first two; we can specify this using the Hexagonal shorthand in JDFTx.

Additionally, det(M) = 3 which means that we need three atoms in the supercell. We can start with [ 0 0 0 ], [ 0 0 1 ] and [ 0 0 -1 ] in unit-cell fractional coordinates. The first one remains invariant upon transforming to the supercell, as before. Taking the second one as a column vector and multiplying by inv(M) yields [ 1/3 -1/3 1/3 ]. The third one is the negative of the second one, and we end up with the initial supercell geometry (after sorting the atoms by their third coordinate):

lattice Hexagonal 5.23966 12.8345  #a/sqrt(2) and sqrt(3)a in bohrs
ion Pt -0.333333  0.333333 -0.333333   1
ion Pt  0.000000  0.000000  0.000000   1
ion Pt  0.333333 -0.333333  0.333333   1

The layer spacing is 12.8345/3 = 4.3 bohrs, so that 5 layers occupy approximately 21 bohrs. For 15 bohrs vacuum spacing, we need a unit cell length of 36 bohrs. Correspondingly, the scale factor for the third fractional coordinate and the offset between supercell repetitions equals 12.8345/36 = 0.356514. Adding repetitions and dropping extra layers, we then arrive at the geometry:

#Save the following to 111.lattice:
lattice Hexagonal 5.23966 36


#Save the following to 111.ionpos:
ion Pt  0.333333 -0.333333 -0.237676   1
ion Pt -0.333333  0.333333 -0.118838   1
ion Pt  0.000000  0.000000  0.000000   1
ion Pt  0.333333 -0.333333  0.118838   1
ion Pt -0.333333  0.333333  0.237676   1

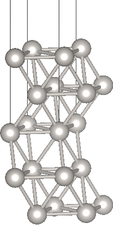
Visualize this geometry using testGeometry.in, JDFTx dry run, createXSF and VESTA as discussed at the end of the Pt(100) setup page to get an image similar to the one above.